The Wonderful World of Mathematics Education 

Mathematics education, as described by mathematician Ronald Brown, includes the realms of description, demonstration, and calculation. Its wide-ranging branches encompass various branches, for example, geometry, which delves into the measurements of lengths, areas, and angles. There’s also arithmetic, which focuses on number theory; mechanics, which interprets the movement of objects influenced by a system of forces and stochasticity, which explores the workings of random phenomena.

In this article, you’ll find a comprehensive overview of the significant milestones and breakthroughs achieved in the field of mathematics throughout history.

The Birth of Math Education

The implementation of mathematics can be traced back to the ancient Egyptians, who were pioneers in its first applications. Consequently, it can be assumed that the earliest mathematics tutors were indeed, the Egyptians. Most notably, archaeological excavations conducted in Mesopotamia during the 19th Century revealed Sumerian clay tablets inscribed with cuneiform script. These tablets date back to either the Babylonian dynasty (1800-1500 BC) or the ancient Greek period (600-300 BC), which sheds light on the mathematical practices prevalent during those eras.

These remarkable artefacts certainly reveal the mathematical prowess of their creators, who displayed proficiency in solving quadratic equations.

In the days of ancient Greece, renowned philosophers such as Pythagoras, Thales, and Plato were instrumental in the development and application of arithmetic, now recognised as number theory in today’s maths terminology. During this period, mathematics education was taken great distances to reach the esteemed city of Alexandria, home to a renowned school. The Library of Alexandria or the Mouseion (Museum) was a centre of knowledge and learning that attracted scholars and intellectuals from various disciplines, including mathematics.

In the 4th century BC, Diophantus of Alexandria played a pioneering role in advancing the discipline of algebra. Subsequently, foundational principles for mathematics education were established by prominent figures like Euclid, Archimedes of Syracuse, and Apollonius of Perge.

Archimedes, an esteemed scientist hailing from Sicily also made significant contributions to geometry. In addition, he made remarkable progress with pi (?), explored the quadrature of the parabola, and introduced the Archimedean spiral. In the realm of statics, Archimedes showed a keen interest in the principle of lift, incorporating pulleys, as well as the design of war machines such as catapults to study the effects of forces. Having said this, he is primarily remembered for his ground-breaking work on buoyancy.

It is worth noting that Archimedes, in addition to his scientific achievements, also had notable engineering endeavours to his name. He was responsible for designing the largest ship of his time, known as the Syracusia. Furthermore, he is credited with the exclamation "Eureka," meaning "I've found it!"

This famous expression is associated with Archimedes and signifies a moment of discovery or revelation.

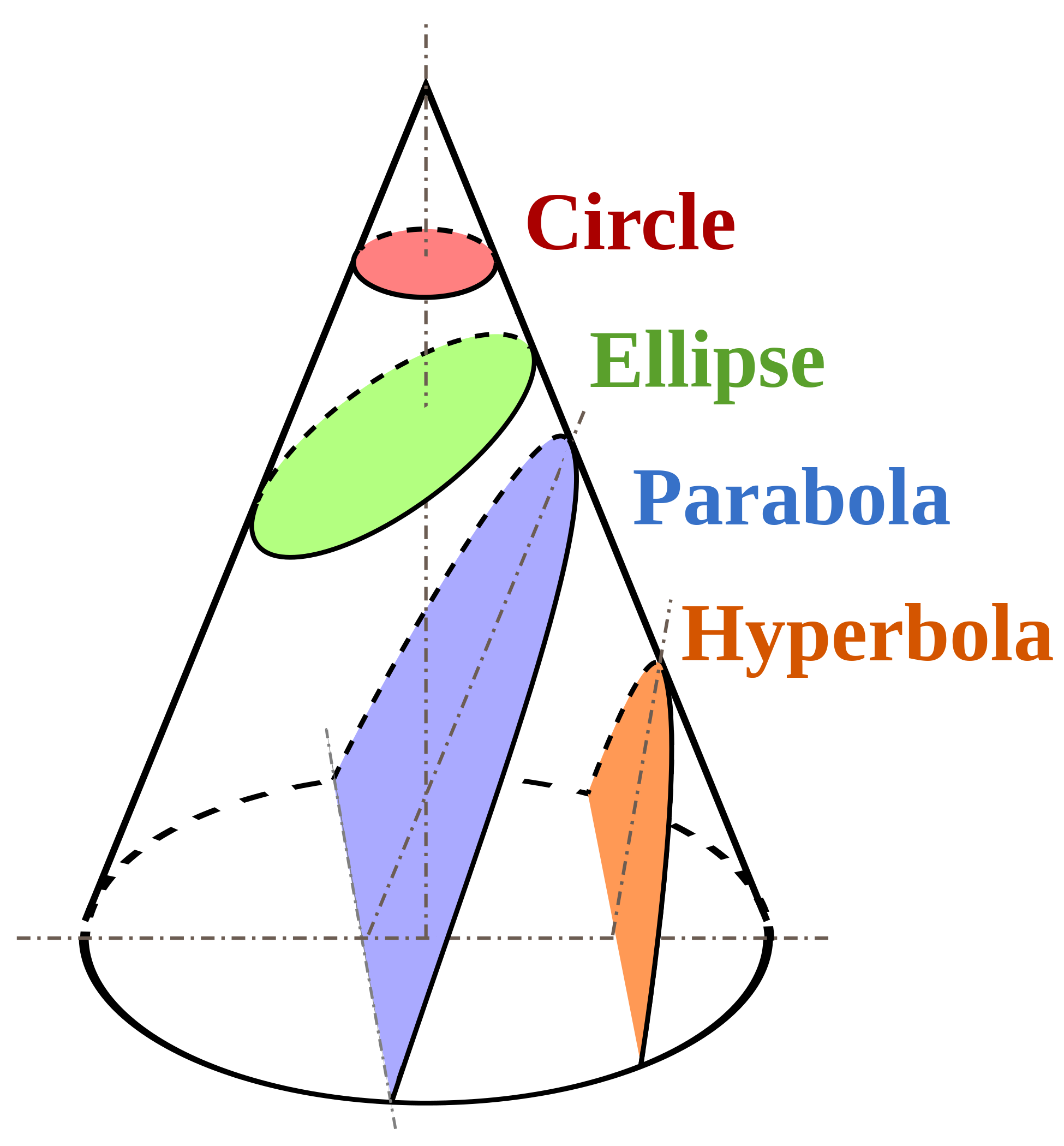
On the other hand, Apollonius of Perga is celebrated for his ground-breaking work in advancing our understanding of conic sections. It is thanks to his contributions that we have the maths terminology for ellipse, parabola, and hyperbola. His work proved to be invaluable not only in mathematics but also in astronomy, aiding in the calculation of eccentric orbits and enhancing our comprehension of planetary motion.

Subsequently, mathematicians such as Ptolemy, Pappus, and Hipparchus played pivotal roles in establishing the foundations of what would later evolve into the field of trigonometry. Trigonometry is concerned with the relationships between angles and distances in triangles, and these scholars made significant contributions to its development.

Furthermore, the concept of zero emerged independently in various civilisations, including India. From there, it spread into Western and Arabic mathematics, profoundly influencing numerical systems and mathematical thinking.

Do you think there's a link between maths and art?

Math Education from the Middle Ages to 1900

If you are looking for maths study materials, don’t forget the history books on the subject!

Arab mathematicians, like Al Khwarizmi, added to Greek and Indian knowledge in the 9th century. In fact, the introduction of Arab numerals in the 11th century heralded the rise of mathematics and increased the recognition of its great thinkers.

From the 12th century, mathematics education gained further prominence over rhetoric, grammar, and logic. Most notably in Spain, scholars like Averroes and Avenzoar rose to fame, teaching Arabic sciences.

So why study maths history?

It’s interesting!

In the 15th century, Johannes Widmann proposed addition and subtraction symbols (+ and -). François Viète's work transformed algebra with the use of letters to represent quantities which simplified equations. Another crazy fact is that Viète's deciphering of a Spanish cipher, albeit with accusations of magic, helped settle the French Wars of Religion.

You will find in your maths study material on history that the 17th century became the golden age of mathematics. Newton's apple sparked the theory of gravity. Notable advances include:

• Neper's Logarithms (1614): This was also known as hyperbolic logarithms. Discover more about this in our guide to maths terminology.
• René Descartes' Analytical Geometry:  In this work, Descartes proposed, as did Viète, that the unity of geometry and algebra translated the question of geometry into algebraic equations. One of the guiding theories in Descartes' process was the need for further clarification on the topic.
• The Calculation of Probabilities by Pascal: Interestingly, gambling was the starting point for the remarkable work of Blaise Pascal!

If the history of maths study material interests you, also check out the work of Euler who is known for his work on functions and calculus during the 18^th century, as well as the contributions of Joseph-Louis Lagrange, for classical and celestial mechanics, number theory and analysis.

Search for A level mathematics lesson with Superprof.

Advances in Math Education Over the Past Two Centuries

Why study maths if all the breakthroughs have happened?

This is a myth, as you go through maths study material you will find that there are many new discoveries waiting to happen. In fact, during this century, math education has been characterised by the completion of 18th-century research.

During the 19^th Century, there were so many great mathematicians that great advances in number theory were made:  A few worth noting include:

• Quadratic reciprocity law
• Arts as theorised by Euler and demonstrated by Gauss.
• Prime number theorem
• Proof of Fermat's Last Theorem, notably by Ernst Kummer for exponents below 100.
• Gauss and Legendre's method of least squares, a significant advancement in statistics and probability.
• Hermann Grassmann's contributions to linear algebra and the concept of vector spaces.
• Urbain Le Verrier's discovery of Neptune and accurate calculation of its mass, which led to the identification of other previously unknown planets.
• Pioneering work on electricity and electromagnetic theory by Gauss, Ampère, and Maxwell.

During the same era, genius mathematician Albert Einstein presented the law of cubic reciprocity, also called the Einstein Integer.

Another noteworthy contribution from this period is Riemann’s 1859 Manuscript which stands as a lasting masterpiece. In it, the German mathematician delved into the Riemann Zeta Function, a concept still crucial in quantum mechanics and number theory and his hypothesis remains highly relevant today.

Later, the 20th century kicked off with a renowned catalogue of 23 unresolved problems that captivated the attention of scientists and mathematicians alike. Throughout this century, three pivotal mathematical theorems emerged as dominant forces:

• dGödel's incompleteness theorems, which presented the question of coherence in maths.
• The Taniyama-Shimura Conjecture, also called modality theorem.
• The Weil conjectures on generating functions.

So how has maths study material changed?

In the 20th century, the continual advancement of mathematics and science led to the appearance of new fields like topology, differential geometry, and algebra. Most notably, mechanics by Einstein and Pointcarré became a focal point of extensive study, resulting in the development of the theory of general relativity.

Group Theory continued to hold the attention of the most brilliant mathematicians for numerous decades, culminating in the exhaustive classification of finite simple groups in 1980. Furthermore, the successful resolution of the Four Colour Theorem was achieved through the invaluable assistance of automated computer calculations.

As the 21st century unfolded, it brought forth momentous breakthroughs, notably spearheaded by the prodigious mathematician Terence Tao, who made astounding advancements in prime numbers and diverse fields.

François Englert and Peter Higgs jointly received the Nobel Prize for Physics on October 8, 2013, for their theoretical discovery of a mechanism that contributes to our understanding of the origin of subatomic particle mass. Interestingly, this scientific breakthrough aligns with a fictional prediction made by Dr Simon Singh in his 2013 book "The Simpsons and Their Mathematical Secrets." In it, Singh noted that a scene in the popular cartoon featured Homer working on an equation that, when solved, yielded a mass for the Higgs Boson very close to its actual value. Homer's prediction, made 14 years prior to the discovery, is a remarkable coincidence.

Despite the excellent progress made in recent decades, you can be sure that there is still an infinite amount of discoveries that are yet to be made.

Embark on a fascinating math journey with an online mathematics tutor! Discover the lives and contributions of great mathematicians and delve into the remarkable advances in number theory. Our expert tutors provide personalized guidance, unraveling the stories behind mathematical breakthroughs and making the complexities of number theory accessible. Enrich your understanding of the subject with engaging discussions and insights. Hire an online mathematics tutor today and let the narratives of great mathematicians inspire your own mathematical exploration!

If you enjoyed this article and want further answers to the question why study maths or want to increase your maths vocabulary, then don’t miss other articles in this series about the correlation between art and maths, math education and computer science and finally, myths and clichés relating to maths.